Nachdem nun endlich ein Konzept entstanden ist und die langweiligen Teile wie die Programmierung der Bewegungen absolviert waren, haben wir angefangen uns dem Algorithmus zu widmen.
Uns war allen bekannt wie der Zauberwürfel per Hand gelöst wird, und auch wie schwierig es ist jemandem das zu erklären. Wie schwer wird es also sein einem Roboter das Lösen des Zauberwürfels beizubringen?
Um die Frage zu beantworten haben Meike und ich angefangen den Algorithmus zu programmieren. Dazu haben wir uns über 1,5 Wochen fast täglich mehrere Stunden lang über Skype getroffen um das Programm zu entwickeln.
Um einen Zauberwürfel zu lösen, geht man oft Ebenen weise vor. Also erst die untere–, dann die mittlere– und zum Schluss die oberste Ebene lösen.

Zuerst muss der Zauberwürfel jedoch im Programm überhaupt erschaffen werden.
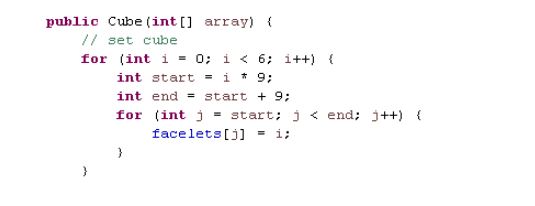
Es wird also für jede der 6 Seiten eine Start– und Endposition im Array festgelegt. Diese Positionen haben eine Differenz von 9, da eine Seite aus 9 Steinen besteht. Die Start-/Endpositionen werden durch eine Laufvariable i bestimmt. Im ersten Durchgang (i = 0) werden also zwischen den Positionen 0*9 =0 und 0+9 =9 im Array die Werte 0 eingetragen. Es entsteht also eine Weiße Seite. Im zweiten Durchgang werden dann nach demselben Prinzip die Positionen von 9 bis 18 mit dem Wert 1 gefüllt, was zu einer orangenen Seite führt, usw. Schließlich entsteht ein gelöster Würfel. Dieser kann durch randomisiertes Drehen der einzelnen Seiten vermischt werden. Das Vermischen haben wir für das Testen in der Online app-Simulation benutzt. Der eigentliche Roboter soll ja nur lösen können.

Aus dem Grund, dass ich den Algorithmus mit Meike zusammen entwickelt habe, können Dopplungen stellenweise auftreten. Um diese möglichst zu vermeiden versuche ich mich daher auf die in ihrem Blog nicht erwähnten Aspekte zu beschränken.
Zurück zum Zauberwürfel! Im ersten Schritt muss die weiße Seite zusammengesetzt werden. Also müssen wir erstmal überhaupt die weißen Kantensteine finden. Für das Suchen von diversen Steinen gibt es daher die Methode findCubie(). Diese wird folgend beschrieben:
Ein Stein(Cubie) kann auf 2 Arten im Array charakterisiert werden. Ein Kantenstein verfügt über 2 Seiten, also hat er auch nur 2 Stellen im Array. Jeder Eckstein hat hingegen 3 Seiten und somit dann auch 3 Stellen im Array.
Das Array “numbers” beinhaltet hierbei die Position (In dem 54 Stellen langen Array) von den Jeweiligen Seite des Steines.

Um einen Cubie zu finden muss also erstmal die Länge des Arrays “numbers” geprüft werden. Bei der Länge 2 werden dann alle Kantensteine in dem Array “edges” abgespeichert. Danach wird für jeden einzelnen Kantenstein (for(Cubie edge : edges)) einmal die folgende Prozedur durchgeführt.
Die Werte von dem Kantenstein (welcher Gerade von dem Programm betrachtet wird) werden im Array “positions” abgespeichert. Folgend wird dann in der if Verzweigung geprüft ob die Farbe des gesuchten Ecksteins mit der Farbe von dem gerade in Betrachtung gezogenen Stein übereinstimmt. Dabei müssen die Farben der beiden Seiten vom gesuchten Stein übereinstimmen, da jeder Kantenstein 2 verschiedene Seiten hat. Deshalb auch 2 Bedingungen in der if-Verzweigung. Falls die Bedingungen Wahr sind wird die Position des Kantensteins zurückgegeben (return edge).
Ähnlich funktioniert das mit den Eckstein (corner , nur das nun auf 3 übereinstimmende Farben geprüft werden muss.
Kurz gesagt, es werden alle Eck-/Kantensteine durchgegangen um diese mit dem gesuchten Stein zu vergleichen.
Problemtisch bei der ersten Ebene ist, das die gesuchten (in unserem Fall weißen) Steine überall im Würfel verteilt sein können. Es muss also eine Möglichkeit geben, jeden weißen Stein aus allen möglichen Positionen am Ende in die eine richtige Lage zu bringen. Da es viel zu aufwendig wäre für jede denkbare Position einen eigenen Algorithmus zu entwerfen und der Roboter sowas nicht wie der Mensch nach Gefühl entscheiden kann, haben Meike und ich unsere eigenen Bewegungen und Algorithmen entworfen.
Es war also sehr schwer einen Algorithmus zu entwickeln, welcher für jeden Fall (auch auf die noch folgenden Schritte bezogen) einen Lösungsweg beinhaltet, welchen auch der Roboter durchführen kann. Es ist erstaunlich, dass 60% des “normalen ” Lösungsweges für den Zauberwürfel ohne Menschliche Intuition nicht möglich wären. Denn es werden immer nur die komplizierten Bewegungen beschrieben, welche einen Stein aus einer gewissen Startposition in die richtige Endposition bringen. Das Bewegen zur Startposition wird nie erwähnt, da man sich Bewegungen wie einmal links drehen selbst denken kann. Jedoch kann man nur anhand von spezifischen Fällen entscheiden ob der Stein einmal nach links, recht, oben oder unten oder sogar 2-mal gedreht werden muss.
Daher verbrachten Meike und Ich einen sehr großen Teil der Zeit, die wir als Gruppe für das Fertigstellen des gesamten Roboters gebraucht haben, um den “allwissenden” Algorithmus zu finden. Das logische Konzept und die Strategie waren hierbei sehr herausfordernd.
Die nächsten 2 Wochen verbrachte ich also damit den Lösungsweg zu finden, wobei wir über Skype dann die Strategie in Quelltext umgesetzt haben. Gleich bekommen Sie einen kurzen Einblick wie Bestandteile eines solchen “allwissenden” Algorithmus aussehen könnten.
Es sind insgesamt sehr viele Schritte also würde eher ein eintöniges Buch entstehen, wenn ich alle Schritte einzeln beschreiben würde. Deshalb werde ich auch gleich nur auf die ersten Methoden eingehen. Falls Sie nicht am Quelltext interessiert sind, muss dieser für das Verständnis auch nicht beachtet werden. Es geht lediglich um einen Einblick in die Entwicklung einer solchen Methode und dessen Dimensionen.

Die erste Methode heißt also “makeSunflower”. Damit ist gemeint, dass alle weißen Kantensteine zur Gelben Seite gedreht werden, wobei die weiße Seite immer auf der gelben Seite drauf sein muss. So könnte nach dem durchführen der Methode die gelbe Seite aussehen:

Wie eine Sonnenblume also. Das sieht am Anfang ziemlich nutzlos aus, ist aber einfach ein Teil einer komplexeren Bewegung.
Es gibt 4 Kantensteine also wird die Methode auch 4-mal durchgeführt (Zeile 598). Hierbei gibt es eine feste Reihenfolge, in der die Steine zur gelben Seite geführt werden. Es wird immer der Stein genommen, dessen eine Seite weiß ist (also 0) und dessen andere Seite die Farbe des Übergabeparameters i besitzt. Am Anfang ist i=1 (also Orange) und im letzten Durchlauf 4 (also Blau).
Danach wird geprüft in welcher Position sich der jeweilige Stein befindet, denn davon hängen die notwendigen Bewegungen ab, die durchgeführt werden müssen um den Kantenstein zur gelben Seite zu bringen.
Der eine mögliche Fall ist, dass der Kantenstein schon auf der gelben Seite ist, wobei jedoch seine weiße Seite nicht oben ist, er ist also falsch ausgerichtet. Wie der weiß-grüne Stein im folgenden Bild.

Hier müsste der Kantenstein also “geflippt” werden, wobei aber die restlichen Bestandteile der Sonnenblume nicht kaputt gemacht werden sollten, was ziemlich herausfordernd war. Hierfür kam schließlich ein erfundener Move ins Spiel (Z.604-623), welcher abhängig davon auf welcher Seite sich der Kantenstein befindet (Z.602) durchgeführt werden kann. Der Stein wird so gesehen einfach umgedreht. Dies geschieht nur falls die weiße Seite nicht nach unten zeigt (sonst wäre sie auf der unten liegenden richtigen gelben Seite) if (! (nicht)numberOnFace(cubie, 0(weiße Seite), Face.DOWN(zeigt nach unten))) (Z.603)
Andererseits könnte der weiß-grüne Stein aber auch wie folgt liegen:

Hierbei müsste die gelbe Seite so lange gedreht werden, bis der freie Platzt direkt über dem grün-weißen Kantenstein liegt, sodass dieser einfach hochgedreht werden kann.
Dazu wird erst mal geprüft, welche Seite überhaupt gedreht werden muss um den Stein hoch zu bewegen, also die Seite auf der die grüne Seite den Kantensteins liegt =(String shortFace = faceOfOtherColor.getNotation()(Z.637).
Die dafür notwendigen Bewegungen hängen auch davon ab, zwischen welchen Seiten, sich der weiß-grüne Kantenstein befindet, also muss die Position auch geprüft werden (Z.626). Danach wird in einer while-Schleife so lange gedreht bis die oben genannte Bedingung stimmt, sodass der Cubie einfach hochgedreht werden kann.
Die dritte Kategorie von möglichen Fällen sieht wie folgt aus: Der grün-weiße Stein ist auf der weißen Seite.

Es wird also wieder zuerst geprüft, wo genau sich der Kantenstein befindet (Z.652). Danach wird die Zielposition bestimmt (Z.654-663). Folgen wird die gelbe Seite in der while-Schleife so oft gedreht, bis die Zielposition direkt über dem Stein ist, sodass dieser einfach 2-mal hochgedreht werden kann. turn(turnClockwise); turn(turnClockwise); (Z.671).
Im zweiten Bild wäre der Stein jedoch immer noch nicht richtig und müsste nochmal geflippt werden. Das wäre genau der erste Fall, also kann man den Quelltext übernehmen (Z.676-696)
So viele Gedanken und Zeilen über einen Schritt welchen man einer Person in 15 Minuten erklären kann.
