Für einen Computer ist eine Funktion wie f(x) = 3x² einfach nur eine einfache Abfolge von Zeichen, mit dem er absolut nichts anfangen kann. So, wie wenn vor dir ein Sack Mehl, eine Tüte Milch, Butter, Zucker und Salz stehen. Was soll man damit? Roh verzehren wohl eher weniger. Es fehlt eine Zubereitung, also eine Ordnung. Die Lösung? Ein binärer Ausdrucksbaum, englisch „Binary expression tree“, kurz BET. In der Informatik ist ein Baum eine Datenstruktur, bei der jeder „Knoten“ (eng.: „Node“) auf maximal zwei weitere Knoten (left & right) zeigt (bzw. sie kennt), diese Nodes nennt man auch „Children“. Ein Knoten ist dabei ein Informationsträger, hier entweder ein mathematischer Operator (+, -, ×, /) oder eine Zahl. Da ein nicht-Hacker mit solchen Begriffen meist nichts anzufangen weiß folgt eine Grafik:
Interpretierung des Baums / Rechnen mit dem Baum
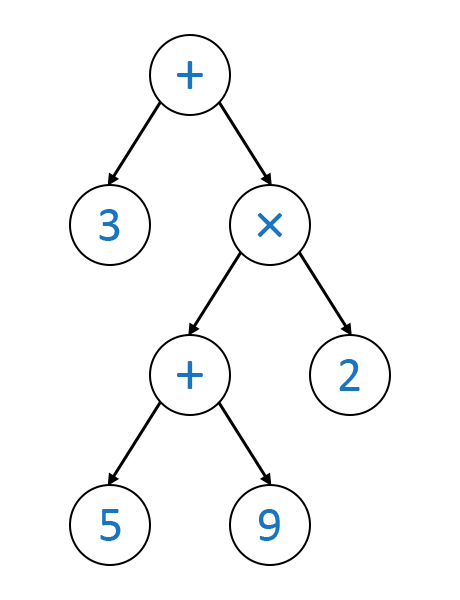
Dieser Baum entspricht dem Ausdruck 3 + (5 + 9) × 2. Wie rechnet der Computer den dann aus? Nun man beginnt ganz oben beim +. Man addiert den linken Knoten (3) mit dem rechten Knoten (×). Davor müssen die Children ausgerechnet werden. Da der linke Knoten dabei schon eine Zahl ist, muss da nichts mehr gerechnet werden. Um den rechten Knoten (×) auszurechnen, müssen wieder die Children ausgerechnet werden: Der linke Knoten (+), der 5 + 9 = 14 entspricht und der linke, der schon eine Zahl ist. Sind beide Children Zahlen-Nodes nach der Ausrechnung, arbeitet sich der Rechner wieder nach oben und rechnet die Zahlen anhand der Node zusammen. Das sieht dann ungefähr so aus:
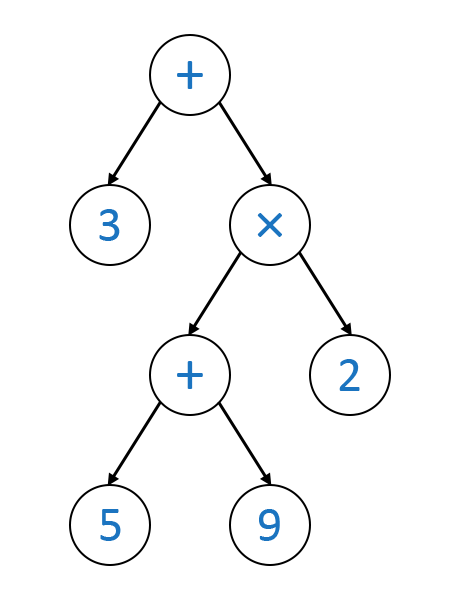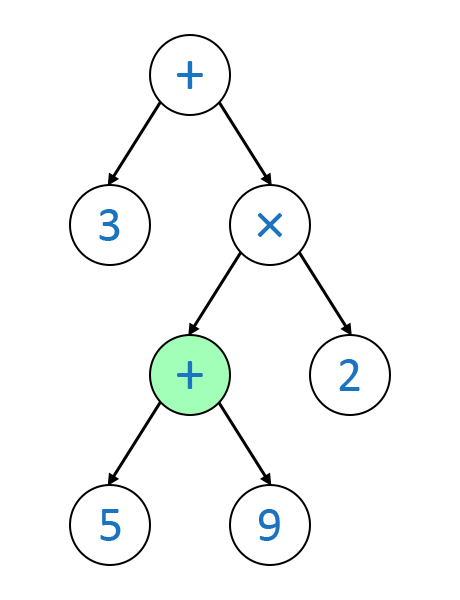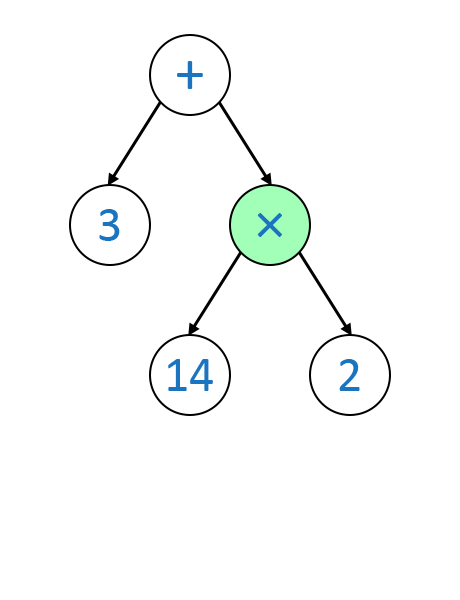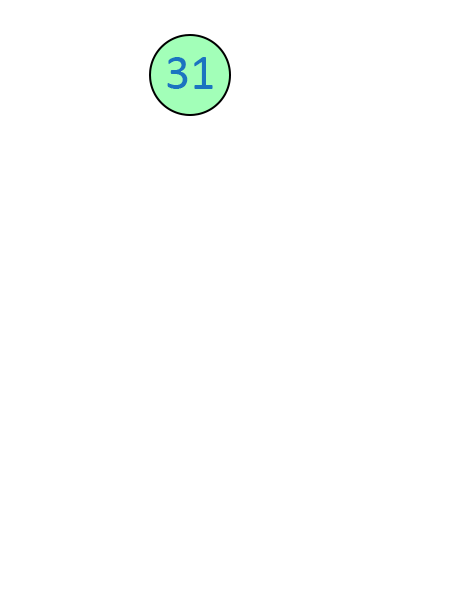
Implementierung und Traversierung
Realisiert wird das dadurch das jeder Knoten eine evaluate-Methode (Beispiel Add-Node) besitzt. Ein binärer Knoten, also ein Knoten mit 2 Children (in dem Fall immer ein Operator-Node) ruft dabei rekursiv die evaluate-Methode seiner Children auf und gibt das jeweilige, abhängig vom Knoten, Ergebnis zurück. Im Endeffekt rufen die Nodes die evaluate-Methode ihrer Children so lange selbst auf, bis sie ganz unten sind, wo ein Zahlenknoten vorzufinden ist. Das ist der Begriff der Rekursivität. Übrigens, der Vorgang einen Baum durchzugehen nennt sich Traversierung (eng.: traversal), wobei nochmal zwischen dem breadth-first traversal und dem depth-first traversal unterschieden wird. In diesen Fall gehen wir zuerst in die Tiefe und dann erst die Breite, also arbeiten wir hier mit einem depth-first traversal.
Ableitung vom Baum
Außerdem wichtig für die Zeichnung der Funktion ist die erste Ableitung (mehr dazu später). Um die zu bilden, hat wie beim Ausrechnen jeder Knoten eine diff-Methode, die die Ableitung des aktuellen Knoten bildet. Auch hier wird rekursiv, abhängig von den Ableitungsregeln, die diff-Methode auf die Children des Knoten ausgeführt.
Dazu zwei kurze Beispiele, wem das zu mathematisch wird kann ruhig diese Sektion überspringen (Meiner Meinung nach aber ziemlich interessant!):
1. Beispiel: Summenregel
Wenn man nun also die Ableitung einer Add-Node herausfinden abfragt, gibt die Add-Node einen neuen Add-Node aus, der die beiden Children jeweils abgeleitet addiert. Code
2. Beispiel: Kettenregel
Diese Regel kommt zum Beispiel beim Sinus-Node vor, dabei ist zu bedenken das der Sinus-Node ein „unary operator“ ist, also nur ein Argument bzw. ein Child kennt. u entspricht hier unserem Sinus und v das beliebige Child der Node. Laut der obrigen Regel muss man für die Ableitung einen Multiplikations-Node erstellen, bei dem der linke Node das Child vom Sinus-Node abgeleitet entspricht und der Rechte die Ableitung von sin(x) aka cos(x) mit dem gleichen Child der Sinus-Node, diesmal nicht abgeleitet. Code
Das wiederholt man nun mit der Ableitung einer Konstanten, der Ableitung von x, der Potenzregel, der Faktorregel, der Differenzregel, der Produktregel, der Quotientenregel und eventuell noch um die Ableitung einer Wurzel, eines Logarithmus und trigonometrischen Funktionen.
Eine wichtige Randnotiz ist zusätzlich das es zum Ableiten sozusagen egal ist was man ableitet, Hauptsache richtig. Beim Beispiel von eben ist es erstmal nicht wichtig für den Sinus-Knoten was sein Child ist, es wird einfach so hingenommen und damit gerechnet. Am Anfang war ich mir dessen gar nicht bewusst und war ziemlich überfragt, wie man nun einen BET ableitet, sobald einem das aber auffällt und nur den Ableitungsregeln befolgt, ist es eigentlich recht einfach. Hehe, kleiner Witz.
